www.batmath.it

Nozioni di topologia in R

In tutta questa monografia si considereranno, di norma, solo funzioni reali di variabile reale, per cui, salvo quando diversamente specificato, il termine funzione sarà usato in questa accezione.

Intervalli

Tra i sottoinsiemi dell'insieme, R, dei numeri reali con la usuale struttura di corpo ordinato ci interesseranno in modo particolare gli intervalli. Se a e b sono due numeri reali, con a<b, adotteremo le seguenti simbologie e definizioni:

 

I numeri reali a e b (solo a nel caso di intervalli illimitati), si dicono gli estremi dell'intervallo. Gli intervalli limitati si chiamano anche segmenti, quelli illimitati semirette. L'intera retta si può considerare un intervallo illimitato sia superiormente che inferiormente.

Intorni

Sia c un numero reale. Si dice intorno di c ogni sottoinsieme di R che contenga un intervallo aperto a cui c appartiene.

Indichiamo con la famiglia di tutti gli intorni di c e mettiamone in evidenza le proprietà essenziali.

A₁) Ogni punto ha almeno un intorno; ogni intorno di c contiene c.
A₂) Se U e V sono intorni di c anche U∩V è intorno di c.
A₃) Se U è intorno di c e se VU, allora anche V è intorno di c.
A₄) Per ogni intorno U di c esiste un altro intorno V di c tale che U sia intorno (oltreché di c) anche di tutti i punti di V.
A₅) Se c e d sono due punti distinti, esistono un intorno V di c ed un intorno U di d tali che U∩V=.

La dimostrazione di queste proprietà è molto facile, ma quello che qui ci interessa segnalare è che molti risultati della teoria dei limiti e della continuità sono legati esclusivamente alla validità di queste proprietà " topologiche", più che al modo specifico con cui gli intorni sono stati definiti. 

La proprietà A₅ è molto importante e garantisce la validità del teorema di unicità del limite che vedremo più avanti. Essa è l'espressione formale del fatto che l'insieme R, su cui è stato introdotto il  citato concetto di intorno, è uno Spazio topologico separato, nel senso che punti diversi possono avere intorni diversi.

Per tutte le applicazioni di cui avremo bisogno non ci servirà un concetto di intorno così generale, ci basterà la seguente definizione semplificata: chiameremo intorno di un numero reale c ogni intervallo aperto che contenga c. In  termini formali si potrebbe dire che ci limiteremo a considerare solo una "base di intorni". Nel seguito il termine intorno sarà sempre riferito a questo concetto semplificato e gli intorni saranno indicati con U_c, V_c o simboli simili.

Avremo anche bisogno, per certe applicazioni, del concetto di intorno destro e di intorno sinistro di un dato numero reale c: un intorno destro è l'intersezione tra un intorno di c e l'insieme degli x>c,  un intorno sinistro è l'intersezione tra un intorno di c e l'insieme degli x<c. I nomi derivano dal fatto che, nella usuale rappresentazione dei numeri sulla retta, un intorno destro sta tutto "a destra", un intorno sinistro sta tutto "a sinistra" di un dato punto c.

Il concetto di intorno permette di introdurre in analisi il fondamentale concetto di "vicinanza" in maniera rigorosa: se c è un numero reale e U ne è un intorno, allora la relazione xU esprime il fatto che x è vicino a c, dove il grado di questa "vicinanza" è dato appunto dall'assegnazione dell'intorno U. Si noti, per esempio, che se come intorno di un dato c prendiamo tutta la retta reale (cosa perfettamente lecita) allora ogni x è vicino a c secondo questo "grado di vicinanza". D'altro canto questo succede anche nel linguaggio comune: due persone possono essere "vicine" anche se si trovano su punti opposti del nostro pianeta, dipende da qual'è il "grado di vicinanza" che vogliamo prendere in considerazione (per esempio quello del vincolo famigliare: le due persone potrebbero essere padre e figlio).

Punti di accumulazione, di frontiera, ecc.

Se A è un sottoinsieme di R (o in generale di uno spazio topologico) e c è un numero reale (anche ad A), diremo che c è un punto di accumulazione per A se U_c l'insieme U_c∩A\{c} è non vuoto.

L'insieme di tutti i punti di accumulazione per un insieme A si chiama derivato di A e si indica con DA, o con D(A).

É di grande importanza pratica la seguente proprietà : In R (e in generale in uno spazio topologico separato) un punto c è di accumulazione per un insieme A se e solo se U_c l'insieme U_c∩A contiene infiniti punti.

Detto in altri termini un punto è di accumulazione per un insieme A se "vicino quanto si vuole" (cioè vicino secondo un qualunque grado di vicinanza) al punto ci sono infiniti punti dell'insieme A.

Come esempio possiamo considerare l'insieme 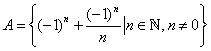. Una rappresentazione grafica, necessariamente sommaria, di questo insieme è la seguente, dove i punti sono rappresentati con dei piccoli rombi e la retta reale ha solo valore di riferimento:

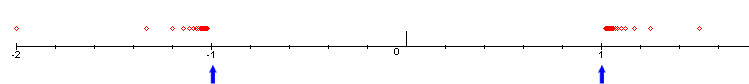
Come si può osservare dalla figura i punti si "accumulano" intorno ai numeri -1 e 1, senza peraltro mai raggiungere questi valori. Questo significa che se si considera un qualunque intorno di -1 o di 1, in essi cadono infiniti punti dell'insieme A: -1 e 1 sono punti di accumulazione per A e sono gli unici punti con questa caratteristica. Si osservi come questi punti non appartengano ad A. 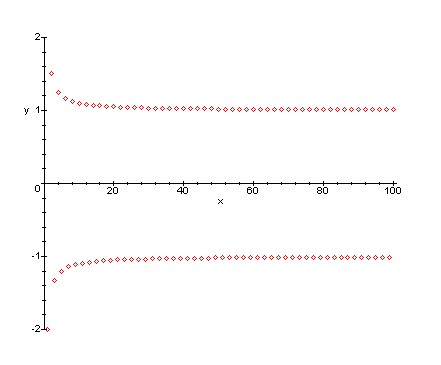Per avere una rappresentazione grafica più significativa e che ci sarà utile in seguito si può osservare che l'insieme A che stiamo considerando può essere visto come l'insieme immagine della funzione . Se si rappresenta graficamente questa funzione e si tiene conto che il suo insieme immagine si può pensare come la "proiezione" del grafico sull'asse delle ordinate, si capisce ancora meglio la struttura dell'insieme A stesso e il fatto che, al crescere di n, i punti dell'insieme si accumulano intorno a 1 e a -1.

Come secondo esempio consideriamo l'insieme dei numeri naturali non nulli: una sua rappresentazione grafica rende subito evidente che in questo caso non esiste alcun punto di accumulazione:

Nel seguito avremo principalmente a che fare con insiemi costituiti da intervalli o unioni finite di intervalli. Nel caso degli intervalli sono punti di accumulazione tutti i punti dell'intervallo, compresi gli eventuali estremi. Questa considerazione ci faciliterà molto il lavoro.

Dato un sottoinsieme A dell'insieme R dei numeri reali ci servirà anche la seguente classificazione dei reali in relazione all'insieme A:

Un punto appartenente all' insieme A, che non sia di accumulazione per A, si dice isolato in A. Si noti che mentre un punto di accumulazione può appartenere o no all'insieme, un punto isolato è sempre un punto dell'insieme. La caratteristica di un punto isolato è che, tra tutti i suoi intorni, ve n'è almeno uno in cui non ci sono altri punti di A al di fuori di lui. Nel caso degli intervalli non ci sono punti isolati. Si noti come la definizione di punto isolato sia, in un certo senso, complementare a quella di punto di accumulazione.

Un numero reale c (che può appartenere o no all'insieme A) si dice punto di frontiera per A se ogni suo intorno contiene sia punti di A che punti del complementare. Nel caso degli intervalli sono di frontiera solo gli estremi dell'intervallo. Questo fatto dà una giustificazione intuitiva del nome utilizzato per questo tipo di punti.

Un numero reale c appartenente ad A si dice interno ad A se esiste un suo intorno tutto contenuto in A. Si noti la differenza tra il concetto di appartenenza (che non ha nulla a che vedere con la topologia) e quello di punto interno.

Un numero reale c si dice esterno ad A se esiste un suo intorno che non ha alcun punto in comune con A.

A proposito di questi concetti valgono alcune proposizioni che è utile dimostrare e che chiariscono il significato delle definizioni date.

copyright 2000 et seq. maddalena falanga & luciano battaia

pagina pubblicata il 07/12/2002 - ultimo aggiornamento il 01/09/2003