Definizione 
Il problema di cui vogliamo occuparci è, sostanzialmente, il problema inverso della derivazione: data una funzione f, trovare, se esiste, un'altra funzione F, la cui derivata sia uguale alla funzione f data: la funzione F sarà chiamata primitiva della funzione f. Come spesso succede per i problemi "inversi", anche questo è un problema tecnicamente molto complesso: le strategie che considereremo non permettono di risolverlo se non in un limitatissimo numero di casi. Per contro, da un punto di vista teorico il problema è abbastanza semplice e si può compendiare nella seguente
Definizione
Sia 
, una funzione definita in un
intervallo I di R. Una funzione
derivabile 
si dice una primitiva
di f se, per ogni x di
I si ha F'(x)=f(x).
Osservazioni
- Si noti che la funzione f è definita su un intervallo e che la funzione F (per potersi chiamare primitiva) deve avere derivata uguale a f per ogni punto dell'intervallo. Se per esempio è data la funzione f(x)=sinx, che vale 0 per x=0, e consideriamo la funzione F(x)=x2, essa ha derivata nulla per x=0: si ha cioè F'(0)=f(0). Questo però non attribuisce alla funzione F il diritto di essere chiamata primitiva di f (ovviamente!). Tutto questo implica che, mentre ha senso parlare di derivata di una funzione in un punto, non ha alcun senso parlare di primitiva di una funzione in un punto.
- Si potrebbero dare definizioni meno restrittive di primitiva: una delle possibilità è che la derivata di F debba essere uguale ad f su tutto I tranne che su un insieme numerabile. Questo tipo di definizione esula però dallo scopo di questa monografia e noi ci atterremo sempre alla definizione più restrittiva data sopra.
- Una delle conseguenze fondamentali della teoria dell'integrale di Riemann è che ogni funzione continua ammette primitive: ciò significa che l'operatore primitiva è molto meno esigente dell'operatore derivazione.
Prime proprietà
- Come conseguenza di un corollario del teorema di Lagrange, se una funzione ha, in un intervallo, due primitive F e G, esse differiscono per una costante. E' poi ovvio che, se F è una primitiva, anche ogni altra funzione F+c (dove c è una costante additiva arbitraria) è una primitiva. Se ne deduce che l'insieme di tutte le primitive di una funzione, in un intevallo, è noto non appena si conosca una primitiva qualunque.
-
Come conseguenza del teorema di Darboux, se una
funzione ha, in un intervallo, una discontinuità a
salto non può avere primitive. Per esempio la funzione
signum(x) non ha primitive in un intervallo
comprendente l'origine. Naturalmente essa può
benissimo avere primitive su un intervallo diverso; per
esempio sui reali positivi una sua primitiva è la
funzione identica f(x)=x. Si tenga presente che
questa caratteristica è propria delle funzioni
definite su un intervallo: per esempio la funzione
f(x)=x/|x| ha primitive (una è la funzione
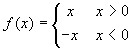), ma essa non è definita in
un intervallo.
Osservazioni sulle notazioni
Sono in uso diverse notazioni per indicare le primitive di una
funzione f. Le più comuni sono quelle che
utilizzano il simbolo di integrale: 
, oppure 
, o ancora (e questa
è in assoluto la più frequente) 
. Precisamente si pone
.
Si noti come i simboli indicati rappresentino un insieme di
funzioni e non una singola funzione. Per esempio si ha: 
. La scrittura
si legge: integrale indefinito
di f(x) in dx. La funzione f si
chiama anche funzione
integranda.
La notazione è quella che ha
avuto più fortuna, in quanto particolarmente utile nel
cambiamento di variabile o quando si considerano funzioni di
più variabili. Si deve però ricordare che il
simbolo dx non è un differenziale: esso ha
sostanzialmente la funzione di un delimitatore finale del
simbolo (una specie di parentesi chiusa).
Tutte le notazioni che usano il simbolo di integrale, 
, hanno poi lo svantaggio di favorire la erronea
identificazione di due concetti, quello di primitiva e quello di
integrale "definito", sostanzialmente diversi, anche
se collegati dal cosiddetto Teorema fondamentale del
calcolo.
In ogni caso la consuetudine vince, e anche noi ci atterremo a queste notazioni, segnalando che preferiamo quelle che non usano il dx. C'è poi un motivo non secondario che fa preferire questo tipo di notazione ad altri: suo padre è nientemeno che Leibniz e riteniamo giusto dare il doveroso tributo di riconoscenza ad uno dei fondatori del calcolo infinitesimale, anche mantenendo le notazioni da lui proposte.